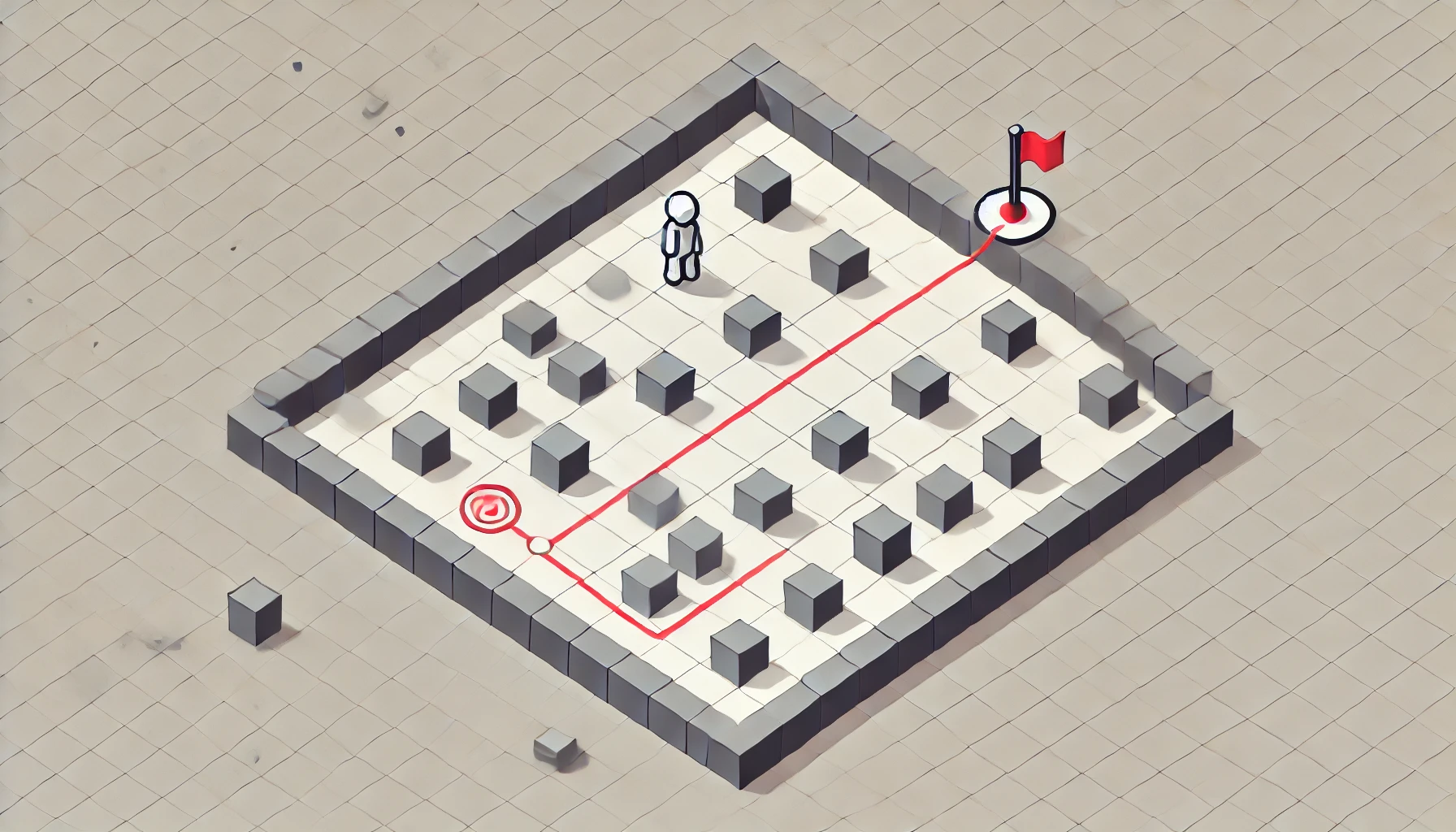
How can video game characters navigate mazes, obstacles, and confusing settings? Did you ever give it a shot? It's all because famous and effective, the A* algorithm which is vital for pathfinding. So, let us understand how A* works and how to apply it to a grid-based game.

 

Understanding A* Algorithm

Strong A* discovers the shortest map route between a start point and a destination while avoiding obstacles. Dijkstra's algorithm and heuristics help A*. A path's total cost is g-cost (the start node cost), h-cost (a heuristic estimate of the goal distance), and f-cost (g + h). A* selects the best path without examining distant routes by analyzing nodes based on these values.

Setting Up the Grid

A* implementation requires a grid-based game map. Algorithms explore walkable grid cells for the optimum target approach. Let's discuss a simple Python grid initialization:

grid_width, grid_height = 10, 10
grid = [[' ' for _ in range(grid_width)] for _ in range(grid_height)]

Each cell in this 10x10 grid is started as a blank area, symbolizing walking ground. Marking cells as obstacles ('#') and starting (S) and goal (G) points is possible later.

Implementing A* in a Grid-Based Game

After creating our grid, let us implement A*. Here are the general steps: 

• Initialization: Add start and goal nodes to the open list of nodes to investigate.
• Node Expansion: Calculate surrounding nodes' g-cost (starting distance) and h-cost (heuristic target estimate). Include them if they are not on the open list or a better route appears.
• Path Reconstruction: After reaching the goal, recreate the path by following parent nodes back to the start.

Here's a simple implementation of the A* algorithm in Python:

class Node:
 def __init__(self, x, y, g, h, parent=None):
 self.x = x
 self.y = y
 self.g = g  # Cost from start
 self.h = h  # Heuristic estimate to goal
 self.f = g + h  # Total cost
 self.parent = parent

def a_star(start, goal, grid):
 open_list = [start]
 closed_list = []
 while open_list:
 current_node = min(open_list, key=lambda node: node.f)
 if current_node == goal:
 # Path found, reconstruct path
 path = []
 while current_node:
 path.append((current_node.x, current_node.y))
 current_node = current_node.parent
 return path[::-1]
 open_list.remove(current_node)
 closed_list.append(current_node)
 for neighbor in neighbors(current_node, grid):
 if neighbor in closed_list:
 continue
 tentative_g = current_node.g + 1  # Assuming uniform cost
 if neighbor not in open_list or tentative_g < neighbor.g:
 neighbor.g = tentative_g
 neighbor.h = heuristic(neighbor, goal)
 neighbor.f = neighbor.g + neighbor.h
 neighbor.parent = current_node
 if neighbor not in open_list:
 open_list.append(neighbor)
 return []  # No path found

Optimizations and Enhancements

We can use a priority queue (min-heap) to manage the open list and identify the node with the lowest f-cost to speed up the A* algorithm. Heuristics like Manhattan distance or diagonal distance can also be changed to work better with specific types of maps.

Conclusion

The A* algorithm for grid-based AI pathfinding is flexible and efficient. It finds the best path without excessive investigation by balancing movement cost with heuristic estimations. Try A* in your game and see your AI explore any map flawlessly!