November 05, 2024
Implementing Gradient Descent in Java: A Practical Approach
Machines learn to predict or make functions perform better, even though how? An essential part of many machine learning algorithms is their gradient descent optimisation technique. This technique is critical in data science and artificial intelligence because it helps find the best parameters for a model by reducing error. So, let's learn how to build the gradient descent algorithm in Java with a complete coding guide.
Understanding Gradient Descent
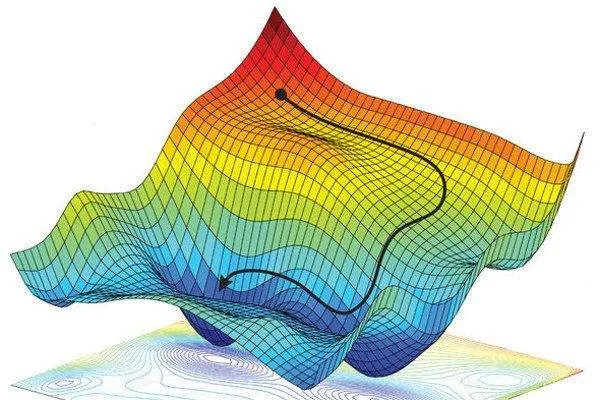
Iterative optimisation algorithms like gradient descent helps you to find the minimum cost function that measures how model's predictions are different from actual results. The first step is to find the cost function's gradient, called its slope. Since the gradient goes toward the highest rise, going in the opposite direction lowers the cost.
The critical parameter of this algorithm is the learning rate. It tells you how big the steps taken to reach the least minimum. Too high or too low a learning rate could lead the minimum to achieve too quickly or slow the convergence, respectively. So, finding balance is key to effective optimisation.
Steps to Implement Gradient Descent in Java
To implement gradient descent in Java, follow these steps:
Define the Cost Function
First, set the cost function you wish to cut most. MSE can help you do this, a most prominent regression metric. It calculates the average squared prediction-actual difference.
Calculate Gradient
After setting the cost function, calculate its gradient. For linear variables, you can use simple differentiation. As parameters vary, the gradient illustrates how much the cost function changes.
Update the Parameters
After that, let's update the parameters (or weights) using the formula:
Theeta_new= Theeta_old - Alpha x gradient
Iterate Until Convergence
Now, repeat these steps unless the change occurs in the cost function becomes negligible. This shows that you've achieved the convergence.
Sample Code Implementation
Here's a simple implementation of the gradient descent algorithm in Java to optimise parameters for a linear regression model.
public class GradientDescent {
public static double gradientDescent(double[] X, double[] Y, double alpha, int iterations) {
double weight = 0;
for (int i = 0; i < iterations; i++) {
double gradient = 0;
for (int j = 0; j < X.length; j++) {
gradient += (weight * X[j] - Y[j]) * X[j];
}
weight -= alpha * gradient / X.length;
}
return weight;
}
public static void main(String[] args) {
double[] X = {1, 2, 3, 4, 5};
double[] Y = {2, 4, 6, 8, 10};
double alpha = 0.01; // Learning rate
int iterations = 1000;
double optimizedWeight = gradientDescent(X, Y, alpha, iterations);
System.out.println("Optimized Weight: " + optimizedWeight);
}
}
Challenges and Tips for Efficient Implementation
While implementing gradient descent, developers may face challenges. It is vital to pick the correct learning rate. It is a value that can cause divergence when too high, while it can cause training to take a long time when too low. When the optimisation issue is not convex, gradient descent could get stuck in local minima. Here, Stochastic Gradient Descent (SGD) wins the game by using just a tiny fraction of the input each time and improving generalisation.
Conclusion
Overall, gradient descent is a vital optimisation algorithm in machine learning, and it's easy to use in Java as long as you know the necessary steps, as I mentioned above. So, now it is time to explore libraries with powerful optimisation techniques to improve your implementations as you dig deeper.
816 views
