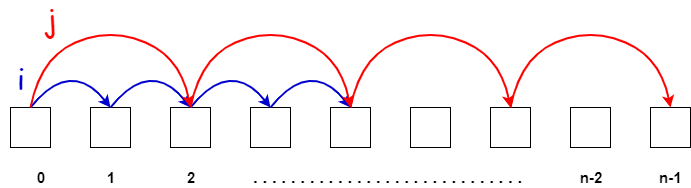
The Two Pointer Technique                                                                                                                                                               

 

Introduction

The two-pointer technique is a fundamental and highly efficient approach for solving problems that involve searching, sorting, or manipulating arrays and strings. It is commonly used when you need to traverse data from both ends, or when you need to compare elements at different positions within a collection. This technique can optimize your solutions time and space complexity, making it a valuable tool for both coding interviews and real-world applications.

In this article, we will explore what the two-pointer technique is, when to use it, and dive into several examples to illustrate its versatility.

 

What Is the Two-Pointer Technique?

In the two-pointer technique, you maintain two different indices (or pointers) that traverse the array or string simultaneously. The pointers can start:

• From both ends of the array and move towards the center.
• From the beginning of the array, with one pointer moving faster or slower than the other.

The goal of using two pointers is to solve a problem in linear time (O(n)), avoiding nested loops that would otherwise result in higher time complexity (like O(n²)).

 

When to Use the Two-Pointer Technique

This technique is most effective when:

1. You need to find pairs or triplets that meet specific conditions (e.g., a sum of elements).
2. You need to modify elements in an array or string in-place (e.g., removing duplicates).
3. You need to compare elements in different parts of an array or string (e.g., checking for symmetry).

Common scenarios include:

• Finding pairs that sum to a target in a sorted array.
• Reversing an array or string.
• Removing duplicates from a sorted array.
• Merging two sorted arrays.
• Detecting a palindrome in a string.

 

Example 1:  Removing Duplicates from a Sorted Array

One of the classic problems that can be solved using two pointers is removing duplicates from a sorted array. The idea is to keep one pointer (j) for tracking unique elements and another (i) for traversing the array.

Here is how it works:

 

 

function removeDuplicates(nums) {
    if (nums.length === 0) return 0;
    
    let j= 1; // The first element is always unique.
// Traverse the array starting from the second element
    for (let i = 1; i < nums.length; i++) {
        if (nums[i] !== nums[i - 1]) {
            nums[j] = nums[i]; // Place the unique element at index j
            j++; // Move k to the next position
        }
    }
    
    return j; // The number of unique elements
}

Explanation:

• i is the pointer that scans the array.
• j is the pointer that stores the position where the next unique element should be placed.
• When a unique element is found (i.e., nums[i] !== nums[i-1]), it is moved to nums[j], and j is incremented.

Time Complexity: O(n)
Space Complexity: O(1)

 

Example 2: Finding a Pair that Sums to a Target in a Sorted Array

In a sorted array, the two-pointer technique can efficiently find a pair of elements that sum up to a given target. Since the array is sorted, we can maintain one pointer (left) starting at the beginning and another pointer (right) starting at the end of the array.

 

 

function twoSum(nums, target) {
    let left = 0;
    let right = nums.length - 1;
    while (left < right) {
        const sum = nums[left] + nums[right];
        if (sum === target) {
            return [left, right]; // Found the pair
        } else if (sum < target) {
            left++; // Increase the left pointer to get a larger sum
        } else {
            right--; // Decrease the right pointer to get a smaller sum
        }
    }
    
    return []; // No valid pair found
}

Explanation:

• left starts at the beginning, and rightstarts at the end of the array.
• If the sum of nums[left] and nums[right]equals the target, return the pair.
• If the sum is less than the target, move left to the right to increase the sum.
• If the sum is greater than the target, move right to the left to decrease the sum.

Time Complexity: O(n)
Space Complexity: O(1)

 

Example 3: Reversing a String

You can also use the two-pointer technique to reverse a string. This is a simple problem where the two pointers start at both ends of the string and move towards the center, swapping characters as they go.

 

 

function reverseString(s) {
    let left = 0;
    let right = s.length - 1;
    while (left < right) {
        // Swap the characters
        [s[left], s[right]] = [s[right], s[left]];
        left++;
        right--;
    }
    return s;
}

Explanation:

• left starts at the beginning of the string and right at the end.
• Swap the characters at left and right, then move the pointers inward.
• Stop when the pointers meet or cross.

Time Complexity: O(n)
Space Complexity: O(1)

 

Example 4: Checking for Palindromes

A palindrome is a word or phrase that reads the same forward and backward. The two-pointer technique can be used to check if a string is a palindrome by comparing characters from both ends.

 

 

function isPalindrome(s) {
    let left = 0;
    let right = s.length - 1;
    while (left < right) {
        if (s[left] !== s[right]) {
            return false; // Mismatch found
        }
        left++;
        right--;
    }
    return true;
}

Explanation:

• left starts at the beginning, and right at the end.
• Compare the characters at left and right. If they are not equal, return false.
• If all the characters match as the pointers move inward, return true.

Time Complexity: O(n)
Space Complexity: O(1)

 

Key Benefits of the Two-Pointer Technique

1. Efficiency: The technique allows you to solve problems in O(n) time without needing nested loops, which often results in O(n²) solutions.
2. Space Optimization: Many two-pointer problems can be solved in-place, avoiding the need for extra memory or auxiliary arrays.
3. Simplicity: The logic behind two-pointer solutions is often intuitive once the setup is correct, making it easier to implement and debug.

 

Conclusion

The two-pointer technique is a powerful strategy that simplifies a wide range of array and string problems. From finding pairs and removing duplicates to reversing strings and checking for palindromes, it offers an efficient way to solve problems that require comparing or manipulating elements within a collection.

Whether you are preparing for coding interviews or optimizing real-world algorithms, mastering the two-pointer technique will improve your problem-solving skills and enhance your ability to tackle complex problems with simplicity and speed